Google的-PageRank 意义与解释(超级网页等级技术)

本文对作为评价甚高的搜索引擎 Google 的核心技术之一 PageRank (网页等级)的基本的概念和评价原理进行解释。

索引

Since: Thu Feb 1 18:22:44 JST 2001
Last Refreshed: Sat Jan 24 18:30:35 JST 2004

★(2007/1/5) 本文的中文版由ROCK翻译制作完成。

★(2003/7/1) 拙著『Namazu系统的构筑和活用』已作修订。详情请看介绍页面。

★(2001/2/28) Namazu 的索引中使用的计算 PageRank 的 Perl 脚本 prnmz-1.0.tar.gz 公开下载。

1.前言

最近，搜索引擎 Google (http://www.google.com/)非常引人注目。Google 是基于现担任 CEO 的 Larry Page 和担任总经理的 Sergey Brin (2001年2月)在就读于美斯坦福大学研究生院时所开发的搜索引擎的一种检索服务。Google 从1998年9月开始服务,但 Netscape Communications 在 Google 的测试阶段就开始与其合作，美国 Yahoo! 公司也从2000年6月起将默认搜索引擎(美国 Yahoo! 不能检索时作为增补的搜索引擎)由原先合作的 Inktomi 转换为了 Google。日语版 Google 在2000年9月正式登场,现已被 BIGLOBE(NEC)所采用。 (注:2001年4月 Yahoo! JAPAN 和 @NIFTY，7月索尼，2002年1月 Excite 也相继与 Google 建立了协作关系)。

Google 被评价的优点不仅仅在于去除无用的(广告)标语构成单一页面的功能、独自的 Cache 系统、动态制成摘要信息、为实现高速检索而设置的分散系统(数千台规模的Linux群集器)等，而其中最大的优点正是它检索结果的正确性。一种能够自动判断网页重要性的技术「PageRank是(网页等级)」就是为此而设计的一种技术。本文的目的就是以尽可能浅显易懂的语言来说明 PageRank 系统的概要和原理。

以下是 PageRank 的一篇基础文章。

Lawrence Page, Sergey Brin, Rajeev Motwani, Terry Winograd, 'The PageRank Citation Ranking: Bringing Order to the Web', 1998,
http://www-db.stanford.edu/~backrub/pageranksub.ps

为了更高效地计算 PageRank,以下是改良以后的一篇论文。

Taher H. Haveliwala, 'Efficient Computation of PageRank', Stanford Technical Report, 1999,
http://dbpubs.stanford.edu:8090/pub/1999-31

另外，以下是 PageRank 的演示用资料(PowerPoint)。

Larry Page, 'PageRank: Bringing Order to the Web',
http://hci.stanford.edu/~page/papers/pagerank/ （已失效）

接下来就对这两篇文章(另加一篇资料)进行基本说明。首先，用简单的例子来解说 PageRank 的概念，再归结到使用超链接关系的排序系统来解决大规模疏松疏矩阵的特性值的问题。然后我们会接触一些在现实世界中应用基本模型时出现的问题和对应方法。接下来，为了探讨是否能够作为「个人化 PageRank」使用，进行对免费全文检索系统 Namazu 的安装实验并对其结果进行阐述。最后发表我对 PageRank 的个人见解。

另外，为了能够理解以下的说明内容，需要大学基础课程程度的数学知识(尤其是线形代数)。然而为使文科生也能够顺利读下去，尽可能地不用算式来说明问题，同时，为了加入笔者个人的见解，没有加入像原文那么多的算法和数字，也存在许多不够严密和欠正确的地方，事先在次声明。具体内容请参照原文。

PageRank^(TM) 是美国 Google 公司的登记注册商标。

2. PageRank 的基本概念

PageRank 是基于「从许多优质的网页链接过来的网页，必定还是优质网页」的回归关系，来判定所有网页的重要性。

在以下冗长的说明中，许多部分大量地使用了专业用语，会造成理解上的困难。这一章虽然准备集中于定性而简单的解说,但是，即使如此也会有怎么也不明白的时候，此时只要能够理解「从许多优质的网页链接过来的网页，必定还是优质网页」这一思考方法也就非常得可贵了。因为在所有几个要点中，这个是最重要的思考方法。

来自于 Google 自己的介绍「Google的受欢迎的秘密(http://www.google.co.jp/intl/ja/why_use.html)」是象以下一样解说的。

关于PageRank
    PageRank，有效地利用了 Web 所拥有的庞大链接构造的特性。从网页A导向网页B的链接被看作是对页面A对页面B的支持投票，Google根据这个投票数来判断页面的重要性。可是 Google 不单单只看投票数(即链接数)，对投票的页面也进行分析。「重要性」高的页面所投的票的评价会更高，因为接受这个投票页面会被理解为「重要的物品」。
    根据这样的分析,得到了高评价的重要页面会被给予较高的 Page Rank(网页等级)，在检索结果内的名次也会提高。PageRank 是 Google 中表示网页重要性的综合性指标，而且不会受到各种检索(引擎)的影响。倒不如说，PageRank 就是基于对"使用复杂的算法而得到的链接构造"的分析，从而得出的各网页本身的特性。
    当然，重要性高的页面如果和检索词句没有关联同样也没有任何意义。为此 Google 使用了精练后的文本匹配技术，使得能够检索出重要而且正确的页面。

通过下面的图我们来具体地看一下刚才所阐述的算法。具体的算法是，将某个页面的 PageRank 除以存在于这个页面的正向链接,由此得到的值分别和正向链接所指向的页面的 PageRank 相加，即得到了被链接的页面的 PageRank。

PageRank 概念图。(引自 Page et al.(1998) Figure 2 'Simplified Page Calculation')

让我们详细地看一下。提高 PageRank 的要点，大致有3个。

反向链接数 (单纯的意义上的受欢迎度指标)
反向链接是否来自推荐度高的页面 (有根据的受欢迎指标)
反向链接源页面的链接数 (被选中的几率指标)

首先最基本的是，被许多页面链接会使得推荐度提高。也就是说「(被许多页面链接的)受欢迎的页面，必定是优质的页面」。所以以反向链接数作为受欢迎度的一个指标是很自然的想法。这是因为，“链接”是一种被看作「可以看看这个页面/这个页会有用」的推荐行为。但是，值得骄傲的是 PageRank 的思考方法并没有停留在这个地方。

也就是说，不仅仅是通过反向链接数的多少，还给推荐度较高页面的反向链接以较高的评价。同时，对来自总链接数少页面的链接给予较高的评价，而来自总链接数多的页面的链接给予较低的评价。换句话说「(汇集着许多推荐的)好的页面所推荐的页面，必定也是同样好的页面」和「与感觉在被胡乱链接的链接相比，被少数挑选出的链接肯定是优质的链接」这两种判断同时进行着。一方面，来自他人高水平网页的正规链接将会被明确重视，另一方面，来自张贴有完全没有关联性的类似于书签的网页的链接会作为「几乎没有什么价值(虽然比起不被链接来说好一些)」而被轻视。

因此，如果从类似于 Yahoo! 那样的 PageRank 非常高的站点被链接的话，仅此网页的 PageRank 也会一下子上升；相反地，无论有多少反向链接数，如果全都是从那些没有多大意义的页面链接过来的话，PageRank 也不会轻易上升。不仅是 Yahoo!, 在某个领域中可以被称为是有权威的(或者说固定的)页面来的反向链接是非常有益的。但是，只是一个劲地在自己一些同伴之间制作的链接，比如像「单纯的内部照顾」这样的做法很难看出有什么价值。也就是说，从注目于全世界所有网页的视点来判断(你的网页)是否真正具有价值。

综合性地分析这些指标，最终形成了将评价较高的页面显示在检索结果的相对靠前处的搜索结构。

以往的做法只是单纯地使用反向链接数来评价页面的重要性，但 PageRank 所采用方式的优点是能够不受机械生成的链接的影响。也就是说，为了提高 PageRank 需要有优质页面的反向链接。譬如如果委托 Yahoo! 登陆自己的网站，就会使得 PageRank 骤然上升。但是为此必须致力于制作(网页的)充实的内容。这样一来，就使得基本上没有提高 PageRank 的近路(或后门)。不只限于PageRank (Clever 和 HITS 等也同样)，在利用链接构造的排序系统中，以前单纯的 SPAM 手法将不再通用。这是最大的一个优点，也是 Google 方便于使用的最大理由。(虽然是最大的理由,但并不是唯一的理由。)

在这里请注意，PageRank 自身是由 Google 定量，而与用户检索内容的表达式完全无关。就像后边即将阐述的一样，检索语句不会呈现在 PageRank 自己的计算式上。不管得到多少的检索语句，PageRank 也是一定的、文件固有的评分量。

PageRank 的定性说明大致就是这样一些。但是，为了实际计算排列次序、比较等级，需要更定量性的讨论。以下一章将做详细的说明。

3.怎样求得 PageRank

我们感兴趣的是，在有像超级链接构造那样的互相参照关系的时候，定量地知道哪一个页面是最「重要」的。换句话大胆地说，这个也就是严密计算「应该从哪一页开始读取」这个指标的过程。就算从谁都不看的小页面开始读取也没有办法。

那么，一般地说为了使得像 Web 那样的超级链接构造能够反映在在排列次序上，需要在计算机上建立超级链接构造的数字模型。怎么模型化需要取决于安装者的方针所以一概而论，但是如果应用图表理论来观察超级链接构造的话，最终常常回到线形代数考虑方法上去。这对于 PageRank 也是一样的。

计算方法的原理

作为最基本的考虑方法，就是用行列阵的形式来表达链接关系。从页面 i 链接到另一张页面 j 的时，将其成分定义为1，反之则定义为 0 。即，行列阵 A 的成分 a_ij 可以用，

  a_ij＝1 if  (从页面 i 向页面 j 「 有 」 链接的情况) 
      0 if  (从页面 i 向页面 j 「没有」链接的情况)

来表示。文件数用 N 来表示的话，这个行列阵就成为 N×N 的方阵。这个相当于在图表理论中的「邻接行列」。也就是说，Web 的链接关系可以看做是采用了邻接关系有向图表 S。总而言之，只要建立了链接，就应该有邻接关系。

(*注)由点和点连接的线构成的图形被称为「图表(graph)」。这些点被称为「顶点(vertex)」或者「节点(node)」；这些线被称为「边(edge)」或者「弧(arc)」。图表分为两类，“边”没有方向的图表被称为「无向图表(undirected graph)」，“边”带有方向的图表被称为「有向图表(directed graph)」。把有向图表想像成单向通行的道路就可以了。图表能用各种的方法来表示,但一般用在数据结构上的是「邻接行列(adjacency matrix)」和「邻接列表(adjacency list)」。需要注意的是，如果是无向图表，邻接行列 A 就成为了对称行列,而如果是有向图表，A 就会成为不对称行列。

以下是用位图表示的 Apache 的在线手册(共128页)的邻接行列。当黑点呈横向排列时，表示这个页面有很多正向链接(即向外导出的链接)；反之，当黑店呈纵向排列时，表示这个页面有很多反向链接。

邻接行列的例子(采用了Apache 的在线手册)

PageRank 的行列阵是把这个邻接行列倒置后(行和列互换)，为了将各列(column)矢量的总和变成 1 (全概率), 把各个列矢量除以各自的链接数(非零要素数)。这样作成的行列被称为「推移概率行列」，含有 N 个概率变量，各个行矢量表示状态之间的推移概率。倒置的理由是，PageRank 并非重视「链接到多少地方」而是重视「被多少地方链接」。

PageRank 的计算，就是求属于这个推移概率行列最大特性值的固有矢量(优固有矢量)。

这是因为，当线性变换系 t→∞ 渐近时，我们能够根据变换行列的"绝对价值最大的特性值"和"属于它的固有矢量"将其从根本上记述下来。换句话说，用推移概率行列表示的概率过程，是反复对这个行列进行乘法运算的一个过程，并且能够计算出前方状态的概率。

再者，虽然听起来很难,但是求特性值和固有矢量的值是能够严密分析的一种基础的数学手段。我们能够自由地给矢量的初始值赋值，但是因为不断地将行列相乘，得到的矢量却会集中在一些特定数值的组合中。我们把那些稳定的数值的组合称为固有矢量，把固有矢量中特征性的标量(scalar)称为特性值，把这样的计算方法总称为分解特性值，把解特性值的问题称为特性值问题。

(*注) 对 N 次的正方行列 A 把满足 Ax =λx 的数 λ 称为 A 的特性值，称 x 为属于 λ 的固有矢量。如果你怎么也不能适应行列的概念的话，你也可以考虑 N×N 的二元排列就可以了。同时，也可以把矢量考虑成为长度为 N 的普通的(一元)排列就可以了。

简单的例子

让我们用简单的例子来试着逐次计算 PageRank 。首先考虑一下有像下图表示那样的链接关系的7个HTML文件。并且，这些HTML文件间的链接关系只是闭合于这1-7的文件中。也就是说，除了这些文档以外没有其他任何链接的出入。另外请注意，所有的页面都有正向和反向链接(即没有终点)，这也是后面将提出的一个重要假定,在此暂且不深入探讨。

表示页面间互相链接关系的推移图

首先，把这张推移图图表构造的邻接列表表示为排列式，就有以下式子。即，根据各个链接源ID列举链接目标的ID。

链接源I D 	链接目标 ID
1		2,3 ,4,5, 7
2		1
3		1,2 
4		2,3,5
5 		1,3,4,6 
6		1,5
7		5

以这个邻接列表中所表示的链接关系的邻接行列 A 是以下这样的 7×7 的正方行列。一个仅有要素 0 和 1 位图行列(bitmap matrix)。横向查看第 i 行表示从文件 i 正向链接的文件ID。

A = [
	 0, 1, 1, 1, 1, 0, 1; 
	 1, 0, 0, 0, 0, 0, 0;
	 1, 1, 0, 0, 0, 0, 0; 
	 0, 1, 1, 0, 1, 0, 0;
	 1, 0, 1, 1, 0, 1, 0;
	 1, 0, 0, 0, 1, 0, 0; 
	 0, 0, 0, 0, 1, 0, 0; 
 ]

PageRank 式的推移概率行列 M ，是将 A 倒置后将各个数值除以各自的非零要素后得到的。即以下这个 7×7 的正方行列。横向查看第 i 行非零要素表示有指向文件 i 链接的文件ID(文件 i 的反向链接源)。请注意，各纵列的值相加的和为 1(全概率)。

M = [ 
	0, 	1,	1/2,	0,	1/4,	1/2,	0; 
	1/5,	0,	1/2,	1/3,	0,	0,	0; 
	1/5,	0,	0,	1/3,	1/4,	0,	0; 
	1/5,	0,	0,	0,	1/4,	0,	0; 
	1/5,	0,	0,	1/3,	0,	1/2,	1; 
	0,	0,	0,	0,	1/4,	0,	0;
	1/5,	0,	0,	0,	0,	0,	0;
]

表示 PageRank 的矢量 R (各个的页面的等级数的队列)，存在着 R = cMR 的关系(c 为定量)。在这种情况下，R 相当于线形代数中的固有矢量，c 相当于对应特性值的倒数。为了求得 R ，只要对这个正方行列 M 作特性值分解就可以了。

在分解特性值时有相应的各种各样的数值分析法,但是本文将不在这里对各种方法详细说明，请读者自己去阅读一本恰当的教科书(在你的暑假里一定有这么一本被埋没的教科书)。在此，我们就暂且使用决 GNU Octave 这个计算程序实际计算一下特性值和固有矢量。

(*注) GNU Octave ，是支持数值计算，类似于描述性出色的 MATLAB 的编程语言。扩展后的处理语言更适合于行列演算,但基本上和C语言的语风相像，因此可读性很高。详细请参照 http://www.octave.org/。当然，除了Octave以外 MATLAB 和 Scilab 也是非常不错的语言，但是根据 GPL, Octave 是最容易得到的。

实际举例

下面我们举一个实际例子。如果不太明白以下例子在做什么的话，只要认为我们能够使用 Octave 这个程序来解特性值问题即可。

首先，使用恰当的编辑器制作以下 Octave 脚本。(在行尾加上分号就能消去多余的结果输出，不过，此次为了说明特意去掉了。)

% cat pagerank.m 
#!/usr/bin/octave 
## pagerank.m - 计算 PageRank(TM) 用的简单的 GNU Octave 脚本

##设置计时器。 
tic(); 

##　根据PageRank 的定义，将从文件 i 链接到文件 j 的链接状态的推移概率行列定义为 M(i,j)

M = [
	0,	1,	1/2,	0,	1/4,	1/2 ,	0;
	1/5,	0,	1/2,	1/3,	0,	0,	0;
	1/5,	0,	0,	1/3,	1/4,	0,	0;
	1/5,	0,	0,	0,	1/4,	0,	0;
	1/5,	0,	0,	1/3,	0,	1/2,	1;
	0,	0,	0,	0,	1/4,	0,	0;
	1/5,	0,	0,	0,	0,	0,	0; 
] 
##计算 全部 M 的特性值和固有矢量列的组合。

[V，D]= eig(M)

## 保存与绝对价值最大的特性值对应的固有矢量到EigenVector。
    
 EigenVector = V(:, find(abs(diag(D))==max(abs(diag(D))))) 

## PageRank 是将 EigenVector 在概率矢量上标准化后得到的值。
 PageRank = EigenVector．/ norm(EigenVector,1) 
 
## 输出计算时间。 
elapsed_time = toc()

(2003/7/23:　修正上述脚本的错误。)

误: EigenVector = V(:, find(max(abs(diag(D))))  )
正: EigenVector = V(:, find(abs(diag(D))== max(abs(diag(D)))))

用 Octave 运行这个 pagerank.m 脚本后在标准输出中得到以下结果。

% octave pagerank.m 
GNU Octave, version 2.0.16 (i586-redhat-linux-gnu). 
Copyright (C) 1996, 1997, 1998, 1999, 2000 John W. Eaton. 
This is free software with ABSOLUTELY NO WARRANTY. 
For details, type `warranty'. 


M =
 
0.00000 1.00000 0.50000 0.00000 0.25000 0.50000 0.00000 
0.20000 0.00000 0.50000 0.33333 0.00000 0.00000 0.00000
0.20000 0.00000 0.00000 0.33333 0.25000 0.00000 0.00000 
0.20000 0.00000 0.00000 0.00000 0.25000 0.00000 0.00000 
0.20000 0.00000 0.00000 0.33333 0.00000 0.50000 1.00000 
0.00000 0.00000 0.00000 0.00000 0.25000 0.00000 0.00000 
0.20000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 

V =
 
Columns 1 through 3: 

0.69946 + 0.00000i 0.63140 + 0.00000i 0.63140 + 0.00000i 
0.38286 + 0.00000i -0.28715 + 0.15402i -0.28715 - 0.15402i 
0.32396 + 0.00000i -0.07422 - 0.10512i -0.07422 + 0.10512i
0.24297 + 0.00000i 0.00707 - 0.24933i 0.00707 + 0.24933i 
0.41231 + 0.00000i -0.28417 + 0.44976i -0.28417 - 0.44976i 
0.10308 + 0.00000i 0.22951 - 0.13211i 0.22951+ 0.13211i 
0.13989 + 0.00000i -0.22243 - 0.11722i -0.22243 + 0.11722i 

Columns 4 through 6: 

0.56600 + 0.00000i 0.56600 + 0.00000i -0.32958 + 0.00000i 
0.26420 - 0.05040i 0.26420 + 0.05040i 0.14584 + 0.00000i 
-0.10267 + 0.14787i -0.10267- 0.14787i 0.24608 + 0.00000i 
-0.11643 + 0.02319i -0.11643 - 0.02319i -0.24398+ 0.00000i 
-0.49468 - 0.14385i -0.49468 + 0.14385i 0.42562 + 0.00000i 
-0.14749+ 0.38066i -0.14749 - 0.38066i -0.64118 + 0.00000i 
0.03106 - 0.35747i 0.03106+ 0.35747i 0.39720 + 0.00000i 

Column 7: 

0.00000 + 0.00000i 
-0.40825 + 0.00000i 
-0.00000 + 0.00000i 
0.00000 + 0.00000i 
-0.00000 + 0.00000i 
0.81650 + 0.00000i
-0.40825 + 0.00000i 

D = 

Columns 1 through 3: 

1.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i -0.44433 + 0.23415i 0.00000 + 0.00000i
0.00000 + 0.00000i 0.00000 + 0.00000i -0.44433 - 0.23415i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 

Columns 4 through 6: 

0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.02731 + 0.31430i 0.00000 + 0.00000i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.02731 - 0.31430i 0.00000 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i -0.16595 + 0.00000i 
0.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 0.00000i 

Column 7: 

0.00000 + 0.00000i 
0.00000 + 0.00000i 
0.00000 + 0.00000i 
0.00000 + 0.00000i 
0.00000 + 0.00000i 
0.00000 + 0.00000i 
-0.00000 + 0.00000i 

EigenVector = 
0.69946 
0.38286
0.32396 
0.24297 
0.41231 
0.10308 
0.13989 

PageRank =
0.303514 
0.166134 
0.140575
0.105431 
0.178914 
0.044728 
0.060703 

elapsed_time = 0.063995

Octave 的输出中，特性值被表示为对角行列 D 的对角成分，各个特性值相对应的固有矢量被表示为行列 V 对应列的列矢量。也就是说 M * V = D * M 成立。如果包含复数特性值的话这里的特性值有7个,其中绝对价值最大的特性值 λ 是λ=1。与之相对应的固有矢量为实矢量：

EigenVector = 
	0.69946 
	0.38286 
	0.32396 
	0.24297 
	0.41231 
	0.10308 
	0.13989

即行列 V 的第1列。请注意，这个求得的固有矢量中概率矢量(要素的和等于1的 N 次元非负矢量)没有被标准化，只是矢量的「大小」等于 1。用算式来表达就是，Σp_i ≠1 ，Σ(p_i)²＝1。在这里，对概率矢量进行标准化

PageRank 就是排位了。注意，全部相加的和为 1。计算只用了0.064秒。

求得的 PageRank 的评价

将 PageRank 的评价按顺序排列 (PageRank 小数点3位四舍五入)。

名次 PageRank   文件ID    发出链接ID  被链接ID
  1     0.304     1       2,3,4,5,7   2,3,5,6
  2     0.179     5       1,3,4,6     1,4,6,7
  3     0.166     2       1           1,3,4
  4     0.141     3       1,2         1,4,5
  5     0.105     4       2,3,5       1,5
  6     0.061     7       5           1
  7     0.045     6       1,5         5

首先应该关注的是，PageRank 的名次和反向链接的数目是基本一致的。无论链接多少正向链接都几乎不会影响 PageRank，相反地有多少反向链接却是从根本上决定 PageRank 的大小。但是，仅仅这些并不能说明第1位和第2位之间的显著差别(同样地、第3位和第4位，第6位和第7位之间的差别)。总之，绝妙之处在于 PageRank 并不只是通过反向链接数来决定的。

让我们详细地看一下。ID=1 的文件的 PageRank 是0.304，占据全体的三分之一，成为了第1位。特别需要说明的是，起到相当大效果的是从排在第3位的 ID=2 页面中得到了所有的 PageRank(0.166)数。ID=2页面有从3个地方过来的反向链接，而只有面向 ID=1页面的一个链接，因此(面向ID=1页面的)链接就得到了所有的 PageRank 数。不过，就因为 ID=1页面是正向链接和反向链接最多的页面，也可以理解它是最受欢迎的页面吧。

反过来，最后一名的 ID=6 页面只有 ID=1 的15％的微弱评价,这可以理解为是因为没有来自 PageRank 很高的 ID=1 的链接而使其有很大地影响。总之，即使有同样的反向链接的数目，链接源页面评价的高低也影响 PageRank 的高低。

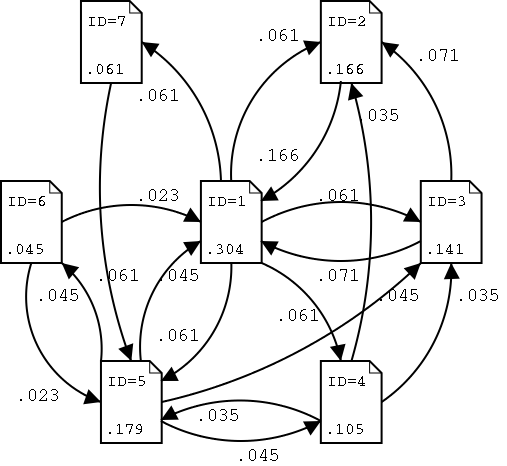表示页面互相的链接关系的推移图(加入了PageRank)

实际地试着计算一下PageRank的收支。因为λ=1所以计算很简单，只要将自各页的流入量单纯相加即可。譬如 ID=1 的流入量为，

流入量＝(ID=2发出的Rank)+(ID=3发出的Rank)+(ID=5发出的Rank)+(ID=6发出的Rank)
    = 0.166+0.141/2+0.179/4+0.045/2
    = 0.30375

在误差范围内PageRank的收支相符合。其他页面ID的情况也一样。以上的 PageRank 推移图正表示了这个收支。沿着各自的链接发出的PageRank等于此页面原有的PageRank除以发出链接数的值，而且和各自的页面的PageRank收支相平衡。

不过，这样绝妙均衡的本身，对理解线形代数的人来说当然不会是让人惊讶的事情。因为这正是「特性值和固有矢量的性质」，总之这样被选的数值的组就是固有矢量。但即使是这样，实际试着确认一下的话，已经能够很好地使用PageRank的方法来考虑了。

以上就是 PageRank 的基本原理。 Google 做的就是大规模地处理这样的非常特性值问题。

4.实际应用时的问题

PageRank 的基本考虑方法并不是很难的东西。实用效果中的巨大成分并不是复杂离奇的算法，而是进行简单的线性变换，倒不如都属于简明直观的类别吧。但是，实际使用 Web 超级链接构造来计算 PageRank 的话，不是简单地能够用嘴巴来说明的东西。主要的困难主要有二个。一、由来于纯粹假设的数值模型和现实世界的不同；二，在实际数值计算上(专门技术的)困难。

准备:数学用语(主要概率过程)的解说

推移概率行列和概率过程上的马尔可夫过程存在很深的关系。本章先离开与 PageRank 本身的说明，预先说明几个呈现在概率过程上的数学用语。因为会设计相当难的部分，如果不能够理解也可以跳过这里。(也可能是我的说明方法不好) 同时，请注意这里几乎没有证明就直接使用了。详细的解说请阅读教科书。

从有向图表S的状态 i 出发，将有限时间之后再次回复到状态 i 的概率作为 1 时，也就是说，当沿着(有向)图表的方向前进能够回到原来位置的路径存在的时候，i 就被成为「回归」。不能回归的状态被称为「非回归」。从状态 i 出发，当通过有限次数的推移达到状态 j 的概率非负的时候，我们就说「从状态 i 到达状态 j 是可能的」。当反方向也可能到达的时候，我们称「i 和 j 互相可能到达」。从状态 i 不能到达其他任何状态的时候，称 i 为「吸收状态」。

从邻接行列 A 所决定的图表(graph)的任意顶点出发，指向其他任意的顶点图表的路径能够像箭头那样到达时被称为「强联结」( 也被称为「分解不能」)。强联结，等价于从任意状态到任意状态可以互相到达。邻接行列 A 的成分中有很多 0 时，强联结性就会有问题。注意，如果全部成分都为 a_ij ≠0 的话，则都属于强联结。因为，对应的马尔可夫链的样本路径表示 S 的任意两点间以正的概率来往通行。

我们可以把全体状态以等价类(或者回归类)来划分。在这里，回归类是指链接所围成的范围。属于一个等价类的状态可以互相到达。从一个类出发以正的概率进入到其他的类的可能性也是存在的。可是很明显，在这种情况下不可能回复到原来的类。不然的话，这两个类就归于等价类了。下图表示了，当 T 作为非回归性的等价类、R 作为回归性等价类时,虽然存在 马尔可夫链 既不来自回归类，也不来自非回归类的情况，但如果一旦来自前两者的话，就不再会回到非回归类中了。

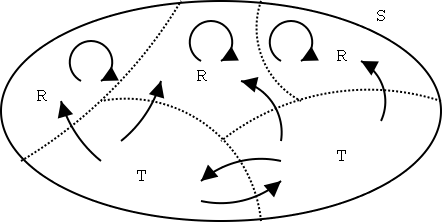回归、非回归示意图(修改了小谷(1997)的图11.1)

这个等价关系中只有一个回归类的时候，那个马尔可夫链就被称为「最简」。换句话说，全部的状态之间互相可以到达时就被称为最简。最简时都是强联结。

互相完全没有关联的邻接行列(或推移概率行列)，乘以恰当的置换行列(掉换行和列)以后得到

P = | P1 0 |
    | 0 P2 |

这样的关系。这表示回归类 P1 和 P2 间完全不存在直接的链接关系。

回归类、非回归类掺杂在一起的邻接行列(或推移概率行列)，乘以恰当的置换行列后得到，

P = | P1 0 | 
    | Q P2 |

这样的关系(Q≠0)。此时，P1是非回归类，P2是回归类。

推移概率行列有时也被称作马尔可夫行列。称马尔可夫过程的试验行列的观测结果为马尔可夫链(Markov chain)。当经过相当的时间后马尔可夫链会趋向某种平衡状态。对任意的状态 i, 如果 j 是非回归状态，则 P_ij⁽ⁿ⁾→0。相反，当 i 为非回归、j 为回归时，停留在状态 i 上着的概率是0。如果 i，j 属于同样的非周期性回归类的话，P_ij⁽ⁿ⁾→P_j≥0。

定理:若 P 是有限马尔可夫行列的话，P 的特性值 1 的重复度等于 P 决定的回归类的数目。(证明太长，省略)。

跟随着推移概率行列的有向图表的最大强联结成分(与之对应的状态的集合)被称为Ergodic部分(历遍部分)，此外的强联结成分被称为消散部分。因为无论从怎样的初期状态概率 x⁽⁰⁾开始，经过时间 n 后 x⁽ⁿ⁾ = P⁽ⁿ⁾x⁽⁰⁾，所以属于消散部分的状态概率几乎接近于0。关于EllGoth部分，连同与各联结成分对应状态的类、像独立的最简的马尔可夫链一样行动，其中，各类中的状态概率(即从过去开始的平均值)的值和初期状态概率无关，换言之，是近似于与对应 P 的最简成分的固有矢量成比例的东西。在类之间概率的分配依存于初期状态的概率。

离散时间型马尔可夫链的不变分布是属于极限分布，从那个分布开始已经不是在分布意义上的随时间的变化了。状态的概率分布在时间变化时也不会变化时被称为固定分布。PageRank 用马尔可夫过程来说就是，PageRank就是以一定时间内用户随机地沿着(网页)链接前进时对各个页面访问的固定分布。

假想模型和现实世界的不同

那么，让我们将概率过程(即图表原理)的考虑方法和实际的网页链接构造合起来看一看。

对于刚才举例的假想网页群来说，只要相互顺着链接前进则在彼此页面间必定有相互链接的关系。即，有向图表是强联结的行列既是回归又是最简。像上面举的很多的概率过程的教科书一样，许多证明都是把回归和最简作为前提来证明的，如果是最简的话，各种各样的性质就变得容易说了。

但是现实的网页并不是强联结。也就是说邻接行列不是最简的。具体来说，顺着链接前进的话，有时会走到完全没有向外链接的网页。通常这样的情况，只有利用 web 浏览器的「返回」功能了。如果人们只是浏览而已的话，一切就到此结束了，然而 PageRank 的计算却不能到此结束。因为PageRank 一旦被引入以后是不能返回的。Pagerank 称这种页面为为「dangling page」。同样道理，只有向外的链接而没有反向链接的页面也是存在的。但 Pagerank 并不考虑这样的页面,因为没有流入的 PageRank 而只流出的 PageRank，从对称性来考虑的话必定是很奇怪的。

同时，有时候也有链接只在一个集合内部旋转而不向外界链接的现象。这是非周期性的回归类多重存在时可能出现的问题。(请读者考虑一下陷入上图中一个 R 中而不能移动到别的 R 和 T 的情况)。 Pagerank 称之为「rank sink」。在现实中的页面，无论怎样顺着链接前进，仅仅顺着链接是绝对不能进入的页面群总归存在，也就是说，这些页面群是从互相没有关联的多数的同值类(回归类)形成的。

总之，由现实的 Web 页组成的推移概率行列大部分都不是最简的。当不是最简时，最大特性值(即1)是重复的，并且不能避免优固有矢量多数存在的问题。换句话说，PageRank 并不是从一个意义上来决定的。

在此，Pagerank 为了解决这样的问题，考虑了一种「用户虽然在许多场合都顺着当前页面中的链接前进,但时常会跳跃到完全无关的页面里」,这样的浏览模型。再者，将「时常」固定为 15％来计算。用户在 85％的情况下沿着链接前进,但在 15％的情况下会突然跳跃到无关的页面中去。(注:Pagerank 的原始手法是各自87％(＝1/1.15 )和13％(＝0.15/1.15)。)

将此用算式来表示的话得到以下公式。

M'= c*M +(1-c)*[1/N]

其中，[1/N]是所有要素为 1/N 的 N次正方行列，c =0.85(=1-0.15)。M'当然也同样是推移概率行列了。也就是说，根据 Pagerank 的变形，原先求行列 M 的特性值问题变成了求行列 M'的优固有矢量特性值问题。M 是固定无记忆信息源(i.i.d.)时，M'被称为「混合信息源」，这也就是固定但非ellGoth信息源的典型例子。

如果从数学角度看，「把非最简的推移行列最简化」操作的另外一种说法就是「把不是强联结的图表变成强联结」的变换操作。所谓对全部的要素都考虑0.15的迁移概率，就是意味着将原本非最简的推移概率行列转换为最简并回归的（当然非负的情况也存在）推移概率行列。针对原本的推移概率行列，进行这样的变换操作的话，就能从一个意义上定义 PageRank、也就是说能保证最大特性值的重复度为1。如果考虑了这样的变换操作的话，因为推移概率行列的回归类的数目变成 1 的同时也最简化，根据前面的定理，优固有矢量(即 PageRank)就被从一个意义上定义了。

数值计算上的问题点(其1)

在此，只要大概明白 PageRank 的概念就可以了，不需要很深的陷入数值计算上的技术的问题中(其实，笔者自己即使有自信也说不清楚)。但是，因为特性值分析和联立一次方程式分析一样，是利用在各种的统计分析中重要的数值计算手法的一中，所以这里我们简单的触及一些分析方法。

主记忆领域的问题是在数值计算上的问题之一。

假设 N 是 10⁴的 order。通常，数值计算程序内部行列和矢量是用双精度记录的，N 次正方行列 A 的记忆领域为 sizeof(double)* N * N =8 *10⁴ * 10⁴＝800MB。 800MB 的主记忆领域不是那种经常会拥有的东西, 虽然这么说也非那种不可能的数字。但是，N 如果变成 10⁵ 或10⁶ 的话，各自就变成80GB,8TB。这样的话不用说内存就连硬盘也已经很困难了。 Google 从处理着10亿以上的页面(2001年时)以来，就知道这种规矩的做法已经完全不适用了。

不过，A 只是稀疏(sparse)行列。因为即使有一部分的页面拼命地进行链接，但是向整个Web展开链接的页面是没有的，即使有也是极为稀少的。平均一下，每一张页面有10-20个左右的链接(根据 IBM Almaden 研究所'Graph structure in the web' 的统计，平均在16.1个左右)。因此，我们可以采用恰当的压缩方法来压缩 A 。 N 即使是 10⁶ 时，如果平均链接数是10，最终的记忆领域只要 80MB，从规模上来说可以收纳到合理的数字里。

稀疏行列的容纳方式当今已经被充分地研究(有限要素法的解法等)，在恰当的数值计算的专业书中就可以学到。虽然这么说，因为相当地难解还是需要很复杂的手法。但想指出的是如果可以很好的解决的话，并列化的高速计算(也许)就变得可能了。因为比起怎样排列并容纳非零要素来说，计算性能和并列性能对其的影响会更大。

数值计算上的问题点(其2)

另一个是收敛问题。

固定方程式

xⁱ＝ΣA_ijx_i

是 N 元的联立一次方程式，一般地不能得到分析解，所以只能解其数值。刚才举的例子中为了求特性值和固有矢量，使用了 Octave 的 eig()函数, 不过，这个在问题小的时候不能适用。说起来，并不需要计算全部的特性值/固有矢量。

求最大特性值和属于它的固有矢量(优固有矢量)的数值计算手法中，一般使用「幂乘法」(也叫反复法)。这是指，取适当初期矢量 x⁰ ，当 x⁽ⁿ⁺¹⁾ = A y⁽ⁿ⁾ (其中 y⁽ⁿ⁾ = x⁽ⁿ⁾ / c⁽ⁿ⁾ )中的 n →∞ 时，x 向拥有最大特性值的固有矢量收敛的同时 c 向此最大特性值收敛的利用线形代数性质的计算方法(证明请参照线形代数的教科书)。幂乘法(反复法)的特长与逐次反复计算的近似法比，能够改善解矢量的问题。它的优点是，因为只要反复对行列和矢量进行适当次数的乘法运算，所以只要通过程序就能够简单地解决，并且还可以进行由于受到内存和硬盘的限制通过直接法不能解决的大规模分析。这是许多的实用算法的出发点。

在这里，请注意从线形代数的简单定理(Peron-Frobenius定理)得到推移概率行列的绝对价值的最大特性值是1。如果采用了这个，就会使得反复法的

PageRank 的计算变得更容易。即，因为最大特性值是既知的，比起求满足 Ax=x 的矢量 x来说，变成更加简单的问题了。这虽然是很细小的地方但是很重要。首先，可以去掉比较花费成本的除法计算 (y⁽ⁿ⁾=x⁽ⁿ⁾/c⁽ⁿ⁾)不用完成。如果是反复法的话，不能得到很高的精确度，并且如果搞错了加速方法的话，计算出的不是是最大特性值而是第二大特性值和属于它的固有矢量(虽然这种情况很少，但是说不定就是从根本上错误的值)。但如果知道了最大特性值，就可以进行核对了。在 Pagerank 的第一篇论文中他们似乎没有注意到这个事情,但在 Haveliwala 的第二论文中增加了关于此的修正。

反复的次数取决于想要求的精度。也就是说,想要求的精度越高，反复的次数就越多。可是，幂乘法(反复法)的误差的收敛比与系数行列的谱段特性(特性值的绝对值分布)有很强的依存关系。具体地说，绝对值最大的特性值用λ₁表示，第二位用 λ₂ 表示，优越率(收敛率 probability of dominance)为 d =λ₁/λ₂ 话，可以知道d离1越近收敛就变得越慢。在 N 很大的情况时d当然离1很近。这是因为，绝对值最大的特性值是1，而其他所有的 N-1 个特性值的绝对值都比1小。但是，N-1个特性值之间非常的拥挤，所以λ₁和λ₂ 之间几乎没有差别。因此一般来说，收敛会变慢。

所谓收敛变慢，严密地说，就是无论经过多少时间也完成不了的计算。对此，为了使收敛加快的适当的加速方法也是存在的，应用这些方法时，需要对数值计算技术有十二分的理解，因此如果不是数值计算的专家就很难引入。

5. Namazu 上的实际安装实验

为了使更简单地推测上文描述的问题，PageRank 并不是非世界所有的web页面而不能使用的考虑方法，即使是个人的利用方法也能实现。为了实现「Personalized PageRank」，针对在各种 UNIX 和 Windows 上运作的中小规模网站适用的全文检索系统 Namazu 进行了实际安装实验。(关于Namazu可参考日语全文检索引擎软件列表。)

由于实验能简单地控制内存的使用量，并将最大特性值用1来考虑，所以将 Have liwala(1999)的想法做为基本的考虑方法。但是对 dangling pages 的处理有少许不同。固有矢量的计算内核使用了数值计算脚本 GNU Octave。所以基本的代码编写自己只用了一天就解决了。另外，从用 mknmz 编写的索引不能直接计算 PageRank，而要事前准备表示邻接关系的索引(邻接列表)。这个也有可能被编入检索者(Indexer)的主要部分。

以下表示了实际计算时间(单位：秒)。运行机器的配置为 PentiumII 400MHz x 2,内存512MB，Kondara MNU/Linux 1.2的(kernel-2.2 .17-15ksmp)，Octave-2.0.16(一般状态分发物)。收敛精度(剩余差矢量的L1规范)取了到1.0e-10,也许有些过分精确了。

文书数N     mknmz时间    准备时间   PageRank计算时间
============================================================
128          58          2          6
2,301       1, 575       46         214
49,604      15,975       478        5,872

因为没用一些巨大的web页群来做测试，所以实验只停留在小规模的基础上。虽然有这个难点,但从基本上可以了解与索引所花的时间相比，在很短的时间里就可以计算 PageRank 的倾向吧。

因为 Namazu 自身中也有很多难题，所以并不寄予很大的奢望，但至少使用 10⁵ 程度(尽可能 10⁶)规模的web页面群来实验。从趋势来看可以预想 N=10⁶ 的计算时间恐怕会发散开去，所以在 N=10⁶ 时，若是能够讨论把mknmz时间变成和comparable一样的加速方法的话，对于Personalized PageRank 来说就十分实用了。作为参考，根据Page et al.(1998)，Google 对7500万的URL的实际 PageRank 计算时间约是5小时。(2001年2月现在不明)。从这个角度来说，研究更加高效的加速法的余地就十分得必要了吧。

计算实际运行时的使用内存最大也是10几MB左右。如果是Haveliwala (1999)那样的「吝啬地作战」的话，最大只有O(3N+2)左右的内存使用量就做完了,不过 N 是 10^4-5 程度和内存的使用量连 N² 也放不进的话，其他的也只能勉强调谐了，所以以 O(5N+α) (α是疏松行列的非零成分数字，典型的是5-20N左右) 程度来编写代码。另外 N 是10³ 左右时，可以确认不压缩疏松行列就在内存上使用幂乘法来计算，从速度面上来说是非常有利的。实测时速度为上述数字的6-7倍左右的。但遗憾的是，这个方法从内存的限制来看，尽可能地只使用2-3千页以内。

此次我们使用了 Octave 分发附属的「Tsurushi」,不过，正像大家知道的那样，如果把 Octave 调谐的好的话，会戏剧性地提高完成的速度。Octave-2.1.x 和 ATLAS 的组合有时候根据情况甚至会使大规模行列乘法的运算速度提高10倍以上。

实验的详细结果请参照prnmz-1.0.tar.gz 中的文档。

Personalized PageRank 的基本性质

人们经常会利用 MHonArc、latex2html 或者 PowerPoint 这样的工具将文档变成 HTML，针对这样的人工制作的HTML链接群求 PageRank 的话，大部分页面的得分几乎都是一样的(～1/N)。如果考虑邻接行列，则大部分的成分是1，或者对角成分附近全部是1。因为这样的推移概率行列的固有矢量成为(1,1,…,1)。

或是象 sitemap.html 一样变成树状的情况下，分数会集中在sitemap.html中。就算占据全体的9成也不算新奇。

从现在起能说的是，为了计算有意义的 PageRank，要尽可能地排除机械生成的链接关系。如果把链接关系看做是推荐关系的话更加容易认同了吧。

6.对 PageRank 的个人的见解

(读者)应该没有余地去怀疑象 PageRank 那样利用超级链接来决定排列次序有效手法吧。

不过，阅读了这些论文以后笔者自身也考虑了许多问题。在这里，列举几个对 PageRank 的个人见解。虽是见解,说到底就是方法论，也许会有很多错误的地方。

关于 dangling page，不相反考虑的原因是什么？

只是因为考虑一定的变异概率时「偶然」会变成最简才不予考虑吗？还是有时看漏了什么吗？稍微有点不太明白。

改善推移概率行列的可能性
说起来，为了保证 PageRank 的单一意义的性质(一意)，只要保证推移概率行列是最简(有向图表是强联结)就行了，没有必要所有的要素 a_ij 都是非零要素。事实上，像在web上浏览 Toyota 汽车网站后紧接着跳向色情网站，接着又继续跳到白宫网站浏览的怪异的人应该是不存在的吧。(请注意这里是指在随时间变化连续的形式)。因此，从实用的意义上来说，区别于改善多少的使用方便程度，应该留下对算法改良的余地。
考虑「逗留概率」会怎样

根据 PageRank 的考虑方法，在一定的时间后必定顺着链接前进到其他的页面，或者突然怪异的、歪曲的跳到其他页面。但是如果对照现实的web浏览模型，也要考虑一定的逗留概率。具体地说，就是推移概率行列的对角成分中只取( 1-c)/N 的话取得过小了。在原本所有变迁概率都一定的情况下，更加进一步分析会怎样？因为对于无聊的页面(浏览者)必定会想都不想就转到另外的页面，反过来对于重要的页面却会停留较长的时间。

如果考虑概率论应用的话必定会考虑其他许多问题

即使是将实现性置之度外，我们也再来试着进一步考虑这个想法。概率论中，存在着一种叫消灭概率或叫固定概率的概率。比起 PageRank 的单纯而同样考虑方法，导入这种考虑方法会得到更期望的结果，所以理所当然被大家所期待。大家都知道马尔可夫链中的分枝过程的考虑方法。这是考虑遗传基因突变时的一个模型，即，说明经过一定的时间而产生淘汰的可能性的模型。很多人认为这个考虑方法或许会被采用。那么导入带有限制的概率(禁忌概率)又会怎么样呢？即，相当于导入通过 n 次的推移从状态 i 移动到状态 j 时，不经过状态 k 的概率。如果考虑到web浏览的性质的话，不是也能理所当然地成为假定吗？

不能作为非马尔可夫过程(或者说 m次的多重马尔可夫过程)来考虑吗

所谓马尔可夫过程，就是与过去的经历无关，只从现在的状态来确定未来的概率法则的概率过程。马尔可夫过程只依存于1步之前的过程。这个过程和没有对过去的记忆，没有依存于过去经历的要素。 PageRank 是在单纯马尔可夫过程随时间变化而固定的状态下计算时候所求得的结果。但是，人类的理性行动必须以非马尔可夫过程来表现。复杂的过程总是以一些形式和过去有着牵连。因此，不仅仅单一地分析从哪个页面连接来，而要分析沿着怎样的路径连接而来的。这样的分析才会使其有可能成为更有用的排序系统。在能抑制住计算量爆炸的范围内，试着引入非马尔可夫过程来研究说不定也很有趣。

在考虑到和看到的许许多多中，有像实际安装那样不太难的东西，也有因为只是嘴上说说而不知道怎样实际安装的东西，不管怎样，定量地评价它的效果是极为困难的。难道真的是不能实现的东西吗？

PageRank 的技术有多少

即使只是采用评价很高的 PageRank 技术，作为基本的想法也只是使用了枯竭的数值分析的手法来实现的。但是，象我在这里说明的事情，如果从专业的研究者来看完全是理所当然的事情了。只是克服规模这一点就能建立一个专业的研究领域吧。也可以认为专业领域的内部并没有那么深的尽头。事实上，我做事，充其量只是表示了「如果是极其小规模的问题，即使是教科书的手法也能大约地得到满足计算量的结果」。

尽管是这样，充其量只触及了概要的表面就在嘴边说「没什么嘛，原来是程度这么简单的技术呀」的那种不懂装懂的人也是有的。在这里事先强调：这种浅薄的看法是从根本上完全错误的。

当然，PageRank 技巧的非常好的地方是「从许多优质的页面连接过来的页面是还是优质的页面」，如果明白了就会觉得是简单的想法。但更进一步说，真正绝妙的地方是，不仅仅只是想到一个主意，而是将想法用固定状态变迁的概率分布来定式化，为了实证其有效性而实际地进行安装实验，并证明其在现实领域也能很好地运作的过程。在所有的这些阶段都成功了才是真正值得被称赞的。

的确，不仅有斩新而且巧妙的想法，再加上结合教科书的手法，也有可能制造出能和 Google 匹敌(或是凌驾)的搜索引擎。也可以说实际上 Google 自己也在这么做着。但是，实际完成的人却是少得惊人。假想模型中的「肯定能够完成」的东西和实际运作的东西之间有着天差地别。在实际问题上，处理大规模疏松行列本身，通过一般的手法也是相当的困难，需要高度的专业技术。应该铭记在头脑中总觉得能够理解的事和实现中能够做的事之间绝对会有不能填埋的差距。不可过分轻率地考虑。

7.参考文献

以下列举了除了在「前言」中介绍的基本论文以外的关联论文。(译者去掉了许多无用的连接)

S. Brin, L. Page, 'The Anatomy of a Large-Scale Hypertextual Web Search Engine', http://www-db.stanford.edu/~backrub/google.html
山名早人，近藤秀和，「解说:搜索引擎Google」(概要) , 信息处理42卷8号(2001年8月), pp.775-780 (PDF)
原田昌纪，「路标:WWW搜索引擎的建立方法」(概要), 信息处理41卷11号(2000年11月), pp.1280-1283
原田昌纪，「搜索引擎检索结果的排序」,bit 2000年8月号(Vol.32), pp.8-14
美国 Clever Project，「聪明地使用超级链接」 (概要) ,日经科学 1999年9月号, pp.28-35
Dell Zhang, Yisheng Dong, 'An Efficient Algorithm to Rank Web Resources', http://www9.org/w9cdrom/251/251.html
Jon M. Kleinberg, 'Authoritative sources in a hyperlinked environment', Proceedings of the 9th ACM-SIAM Symposium on Discrete Algorithms, 1998. http://www.cs.cornell.edu/home/kleinber/auth.ps
IBM Almaden Research Center, 'CLEVER Searching', http://www.almaden.ibm.com/cs/k53/clever.html

以下列举数学关联的参考书籍。

S．卡琳著，佐藤健一，佐藤由身子译，『概率过程讲义』(数理分析与周边3),1974年，产业图书
岩堀信子著，『图表和概率过程』 (与数理分析与周边4),1974年，产业图书
伊藤升他著，『经济系、工学系的行列及应用』, 1987年，纪伊国屋书店, ISBN4-314-00477-0
L.V.Atokinson, P.J.哈里, J.D.赫德森共著，神谷纪生，大野信忠，佐胁丰，北荣辅合译，『数值计算及其应用- FORTRAN77-』, 1993年，Science公司，ISBN4-7819-0690-7
宫泽政清著，『概率和概率过程』(现代数学研究小组17),1993年，近代科学社， ISBN4-7649-1034-9
伊理正夫著，『线形代数II』(岩波讲座应用数学11) ,1994年，岩波书店, ISBN4-00-010521-3
韩太舜，小林欣吾著，『信息和符号化数理』(岩波讲座应用数学13) ,1994年，岩波书店, ISBN4-00-010523-X
小国力著，『MATLAB及其实际利用-现代应用数学和CG -』( Information & Computing=86),1995年，Science公司， ISBN4-7819-0763-6
长谷川里美，长谷川秀彦，藤野清次译，『反复法 Templates』(应用数值计算Library),1996年，朝仓书店, ISBN4-254-11401-X
小谷真一著，『测每次和概率2』(岩波讲座现代数学基础10 ),1997年，岩波书店, ISBN4-00-010640-6
藤野清次著，『数值计算之基础-以数值解法做为中心』(Library新信息工程之基础9),1998年，Science公司，ISBN4-7819-0861-6

与有关 Google 的在线新闻报道(日语新闻)已经分离到其另一张页面(googlenews.html) 。(2003/5/20)

其他，特别列出几个认为有关联的页面。

Interview with Google's Sergey Brin(翻译报道) (LinuxGazette)
Web搜索引擎的商务模型和检索技术动向-以Google为例- (JCOT报告)
聪明地分开使用吧!　21世纪的搜索引擎(InternetWatch)
Web的「地图」的研究成果公布。10％没有被链接 (InternetWatch)
站点研究结果「搜索引擎之检索到了一部分」 (HotWired Japan)
检索引擎的检索结果不平等 (HotWired Japan)
Google --停住时代，你是美丽的--(yomoyomo 氏族)
Google Weblog (Japanese Version)
Patent Death Pending (the cluetrain weblog)
Google's PageRank: Calculator (Web Workshop)

感谢转载！其他许多的个人站点和BBS都介绍了此文。

ZDNet China中文如何提高网站在Google中的排名(2003/1/6报道) 。读不了... :-)
ZDNet China 如何评价一个网站的人气(2002/8/5报道) 还是中文。读不懂... :-)
中村正三郎「BRAVO! Linux」Linux Japan 2001年5月号
InternetWatch Watcher选出的今天的站点2001年3月16日号
InternetWatch 摘要新闻2001年2月26日号
Google World > Japanese >计算机>因特网> WWW >主页检索目录
Lycos /计算机、因特网/因特网/站点的检索、链接集/搜索引擎/机器人检索/ Google 目录
Yahoo! JAPAN 商务经济>企业>因特网服务>企业间交易(BtoB)>检索，导航> Google 目录

8.附录:「guguru？/ goguru?」

英语(美式英语)中是不可能把 Google 念成「goguru」的。和没有人把拉面的 noodle 发音或标记为「nodoru」一样，如果硬要用片假名来表示的话应该写成「グーグル」。

不过，有oo 这个拼写的英文单词有以下这些。

book, bool, cook, cool, food, good, hook, look, loop, loose, mood, moon, noon, pool, roof, soon, tool, wood, zoo, ...

这些都是简单的一般的英文单词,但不论取哪个都有「u:」这个发音。至少，对许多的典型的日本人来说听起来是这样的吧。英语(美式英语)，oo 的拼写基本读成「u」。当然，goo就读成「gu:」。广末凉子不也在中古车信息杂志的电视广告中说「如果要说车，gu―」吗？另外，游泳时使用游泳眼镜的拼写是 goggle。

当然，如果 Google 不是英语(美式英语)话那就另当别论了。但是，Google 名字的由来是从表示10的100次方的英文单词「googol」而来的，也许还是英语发音比较适合(google)吧。不用说，googol 的发音也是「guguru」吧。

另外，创业者之一是 Sergey Brin，从他的名字就能明白他是俄罗斯出身，也有可能是他的英语发音带有自己的方言。如果扯到那里的话，已经是牵强附会了。而且，我也不太清楚Google 用俄罗斯的地方口音怎么发音。如果有识之士在的话，请一定告诉我。

补充(2001/4): 给Google的支持中心发了「是goguru,还是guguru？」的询问信的一位读者，热情地给我转发了这封邮件。对方说虽然 Google 自己本身的发音是「guguru」,不过，你以你自己喜欢的叫法称呼也决不会介意的哦。

Date: Wed,31 Jan 200116:12:01-0800
From:”GoogleTech”<googletech＠google.com>
Subject: RE:{Google#034-917 } pronunciation
To:转送邮件者(Thanks)!

We go by:”GU Gul” 

But you are welcome to say whichever you prefer! 

Regards， 
The Google Team

补充2(2001/10/29):请看Google的页面 ”Google”怎么发音。